dfs
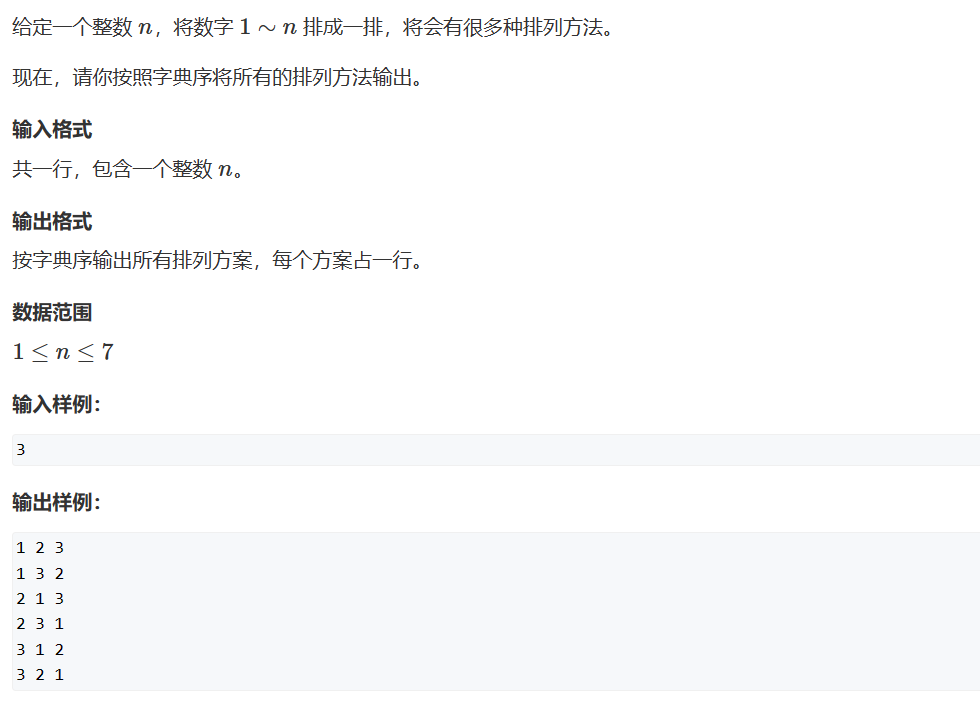
#include<iostream>
using namespace std;
const int N=10;
int n;
int path[N];//存放每一步的数字
bool vis[N];//表示该数字是否被访问
void dfs(int u)
{
if(u==n)//u==n表示每一步已经放好了数字,输出
{
for(int i=0;i<n;i++)cout<<path[i]<<" ";
puts("");
}
else{
for(int i=1;i<=n;i++)
{
if(!vis[i])//判断数字是否被访问
{
path[u]=i;
vis[i]=true;
dfs(u+1);
vis[i]=false;
}
}
}
}
int main()
{
cin>>n;
dfs(0);
}
n皇后

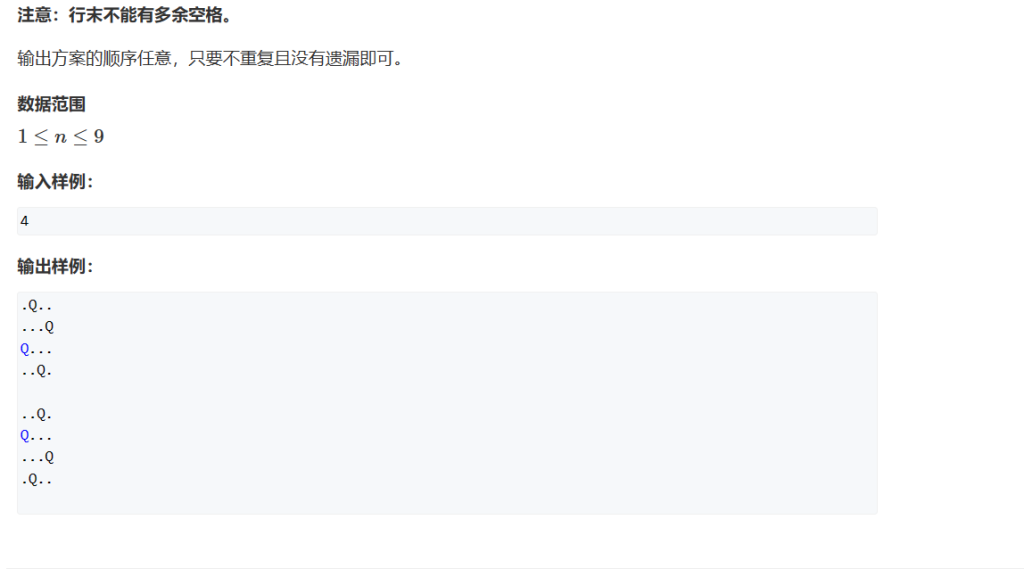
#include<iostream>
using namespace std;
const int N=30;
char m[N][N];
bool r[N],l[N],x1[N],x2[N];
void dfs(int u,int n)
{
if(u==n){
for(int i=0;i<n;i++)
{
for(int j=0;j<n;j++)
cout<<m[i][j];
puts("");
}
puts("");
}
else{
for(int i=0;i<n;i++)
{
if(!r[u]&&!l[i]&&!x1[u+i]&&!x2[i-u+n-1])
{
m[u][i]='Q';
r[u]=true;
l[i]=true;
x1[u+i]=true;
x2[i-u+n-1]=true;
dfs(u+1,n);
r[u]=false;
m[u][i]='.';
l[i]=false;
x1[u+i]=false;
x2[i-u+n-1]=false;
}
}
}
}
int main()
{
int n;
cin>>n;
for(int i=0;i<n;i++)
for(int j=0;j<n;j++)
m[i][j]='.';
dfs(0,n);
}
首先思路,依次给每一行放皇后,判断能否放,能放要满足行列对角线无皇后,然后设置对应数组为true,然后放下一行,这个遍历后要回溯,即把之前改变的变回去
bfs
走迷宫


#include<iostream>
#include<queue>
#include<algorithm>
#include<cstring>
using namespace std;
typedef pair<int,int> PII;//定义打包,这个要学会
int n,m;
const int N=110;
int a[N][N],d[N][N];
int dfs()
{
memset(d,-1,sizeof d);//d初始化为-1
d[0][0]=0;
queue<PII> q;
q.push({0,0});
int dx[4]={0,1,0,-1},dy[4]={1,0,-1,0};//用数组表示偏移
while(q.size())
{
PII tmp=q.front();
q.pop();
for(int i=0;i<4;i++)
{
int x=tmp.first+dx[i],y=tmp.second+dy[i];
if(x>=0&&x<n&&y>=0&&y<m&&d[x][y]==-1&&a[x][y]==0)
{
d[x][y]=d[tmp.first][tmp.second]+1;
q.push({x,y});
}
}
}
return d[n-1][m-1];
}
int main()
{
cin>>n>>m;
for(int i=0;i<n;i++)
for(int j=0;j<m;j++)scanf("%d",&a[i][j]);
cout<<dfs();
}

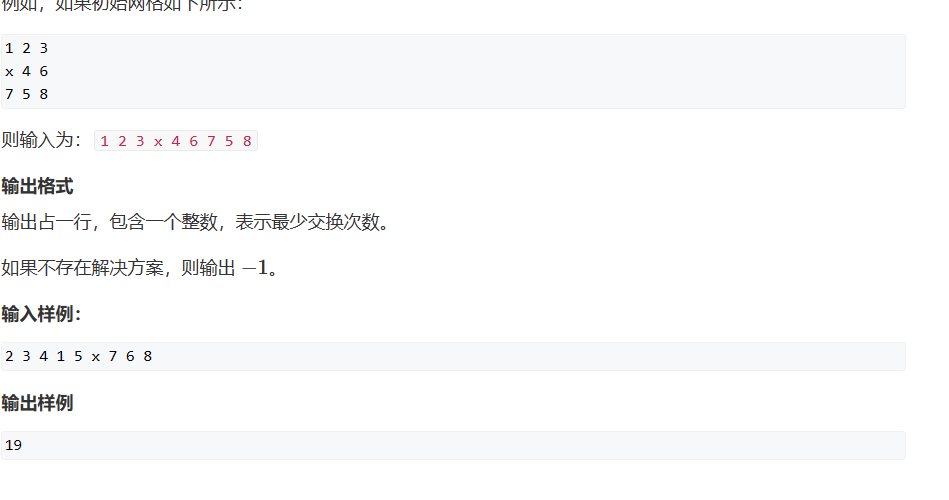
#include<iostream>
#include<queue>
#include<algorithm>
#include<cstring>
#include<unordered_map>
using namespace std;
string s1,s2;
int bfs()
{
queue<string> q;
unordered_map<string,int> d;
q.push(s1);
int dx[4]={0,1,0,-1},dy[4]={1,0,-1,0};
d[s1]=0;
s2="12345678x";
while(q.size())
{
auto tmp=q.front();
q.pop();
int sx=tmp.find('x');
if(s2==tmp)return d[s2];
for(int i=0;i<4;i++)
{
int x=sx/3+dx[i],y=sx%3+dy[i];
if(x>=0&&y>=0&&x<3&&y<3)
{
int distance=d[tmp];
// cout<<distance<<endl;
swap(tmp[sx],tmp[3*x+y]);
if(!d.count(tmp))
{
q.push(tmp);
d[tmp]=distance+1;
}
swap(tmp[sx],tmp[3*x+y]);
}
}
}
return -1;
}
int main()
{
char s[2];
for (int i = 0; i < 9; i ++ )
{
cin >> s;
s1 += *s;
}
cout << bfs() << endl;
return 0;
}
关于邻接表的学习
一、首先 弄清楚 几个数组的含义,然后再去 看 邻接表的表示代码,发现容易理解一些,在这里再次回顾下几个数组的含义:
h[N] : 表示 第 i 个节点的 第一条边的 idx
ne[M] : 表示 与 第 idx 条边 同起点 的 下一条边 的 idx
e[M] : 表示 第idx 条边的 终点
N : 节点数量
M:边的数量
i : 节点的下标索引
idx : 边的下标索引
二、然后结合代码模版理解定义
变量初始化定义:
int h[N], e[M], ne[M], idx;
当我们加入一条边的时候:
public static void add(int a,int b){
e[idx] = b; // 记录 加入的边 的终点节点
ne[idx] = h[a]; // h[a] 表示 节点 a 为起点的第一条边的下标,ne[idx] = h[a] 表示把 h[a] 这条边接在了 idx 这条边的后面,其实也就是把 a 节点的整条链表 接在了 idx 这条边 后面;目的就是为了下一步 把 idx 这条边 当成 a 节点的单链表的 第一条边,完成把最新的一条边插入到 链表头的操作;
h[a] = idx++; // a节点开头的第一条边置为当前边,idx移动到下一条边
}
树和图的深度优先遍历
//对于每个点k,开一个单链表,存储k所有可以走到的点,h[k]存储这个单链表的头节点
// h[N] : 表示 第 i 个节点的 第一条边的 idx
/// ne[M] : 表示 与 第 idx 条边 同起点 的 下一条边 的 idx
// e[M] : 表示 第idx 条边的 终点
// int h[N],e[N],ne[N],idx;
// N : 节点数量
// M:边的数量
// i : 节点的下标索引
// idx : 边的下标索引
//增加一条边a->b;
void add(int a,int b)
{
e[idx]=b,ne[idx]=h[a],h[a]=idx++;
}
//初始化
idx=0;
memset(h,-1,sizeof h);
int dfs(int u){
st[u]=true;//st[u]表示u已经被遍历过
for(int i=h[u];i!=-1;i=ne[i])
{
int i=0;
int j=e[i];
if(!st[j])dfs(j);
}
}

#include<iostream>
using namespace std;
#include<cstring>
#include <algorithm>
const int N=100010,M=2*N;
int e[M],h[N],ne[M],idx;//h表示该顶点的第一条边,e[M]表示该边的终点,ne表示同起点的下一条边
bool st[N];
int ans=N,n;
void add(int a,int b)
{
e[idx]=b,ne[idx]=h[a],h[a]=idx++;
}
int dfs(int u)
{
int size=0;
int sum=0;
st[u]=true;
for(int i=h[u];i!=-1;i=ne[i])
{
int j=e[i];
if(!st[j])
{
int s=dfs(j);
size=max(size,s);
sum+=s;
}
}
size=max(size,n-sum-1);
ans=min(size,ans);
return sum+1;
}
int main()
{
cin>>n;
memset(h, -1, sizeof h);
for(int i=0;i<n-1;i++)
{
int a,b;
scanf("%d%d\n",&a,&b);
add(a,b);
add(b,a);
}
dfs(1);//顶点定义的是1-n,所以要从1开始dfs;
cout<<ans;
return 0;
}
树和图的广度优先遍历
模板
##bfs
queue<int>q;
st[1]=true;//表示第一个节点被遍历过
q.push(1);//从1开始
while(q.size())
{
int t=q.front;
q.pop();//出队
for(int i=h[t];i!=-1;i=ne[i])
{
int j=e[i];
if(!st[j])//将下一步的点都入队
{
st[j]=true;
q.push(j);
}
}
}
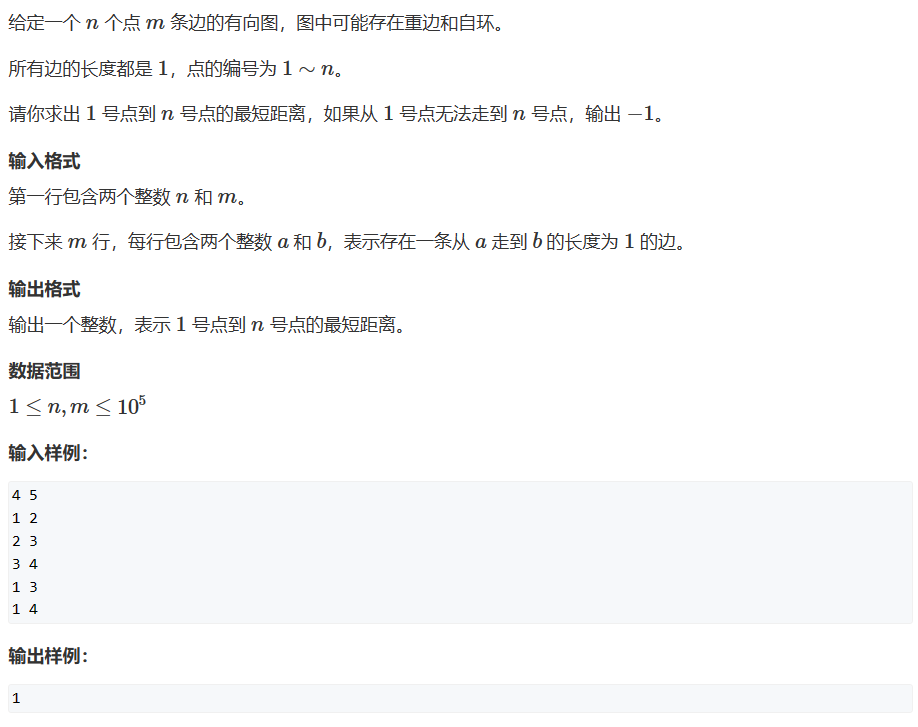
#include<iostream>
using namespace std;
#include<queue>
#include<cstring>
#include<algorithm>
const int N=100010;
int h[N],ne[N],e[N],idx,d[N];
void add(int a,int b)//插入
{
e[idx]=b;
ne[idx]=h[a];
h[a]=idx++;
}
int main()
{
int m,n;
cin>>n>>m;
memset(h,-1,sizeof h);//不初始化下面会超时
memset(d,-1,sizeof d);//初始化,注意位置,一定要先初始化
while(m--)
{
int a,b;
scanf("%d%d\n",&a,&b);
add(a,b);
}
queue<int> q;
d[1]=0;
q.push(1);
while(q.size())
{
int a=q.front();
q.pop();
for(int i=h[a];i!=-1;i=ne[i])
{
// cout<<"dsdffdfd[a]";
int j=e[i];//
if(d[j]==-1){//改变距离,重边和自环无法入队
d[j]=d[a]+1;
q.push(j);
}
}
}
cout<<d[n];
}
另外加一种我的尝试,目前无法解决自环问题
#include<iostream>
#include<cstring>
#include<queue>
#include<algorithm>
using namespace std;
const int N=100010,M=N*2;
int h[N],ne[M],e[M],idx,d[N];
bool st[N];
int n,m;
typedef pair<int,int> PII;
void add(int a,int b)
{
e[idx]=b;ne[idx]=h[a],h[a]=idx++;
}
int main()
{
// typedef pair<int,int> PII;
// unordered_map<PII,int> mymap;
scanf("%d%d",&n,&m);
memset(h,-1,sizeof h);//对不起我是SB这里是初始化h,你不初始化永远跳不出去
for(int i=0;i<m;i++)
{
int a,b;
scanf("%d%d",&a,&b);
// if(!mymap[{a,b}])
// {
add(a,b);
// mymap[{a,b}]++;
// }
}
st[1]=true;
queue<PII> q;
q.push({1,0});
//注意了你这里并不是和你想的一样,首先第一次确实它们都是距离为1,但是第二步呢,每次出队一个边距离就++这时不对的,这并不是距离只能说第几个被遍历的
memset(d, -1, sizeof d);
while(q.size())
{
PII b=q.front();
int dis=b.second;
int a=b.first;
q.pop();
for(int i=h[a];i!=-1;i=ne[i])
{
int j=e[i];
if(!st[j])
{
st[j]=true;
q.push({j,dis+1});
d[j]=dis+1;
}
}
}
cout<<d[n];
}
拓扑排序
bool topsort()
{
int hh = 0, tt = -1;
// d[i] 存储点i的入度
for (int i = 1; i <= n; i ++ )
if (!d[i])
q[ ++ tt] = i;
while (hh <= tt)
{
int t = q[hh ++ ];
for (int i = h[t]; i != -1; i = ne[i])
{
int j = e[i];
if (-- d[j] == 0)
q[ ++ tt] = j;
}
}
// 如果所有点都入队了,说明存在拓扑序列;否则不存在拓扑序列。
return tt == n - 1;
}
dijkstra 算法
int g[N][N];//存储每条边
int dist[N];//存储1号点到每条边的最短距离
bool st[N];//存储每个点的最短路径是否已经确定;
//求1号点到n号点的最短路,如果不存在返回-1
int dijkstra()
{
memset(dist,0x3f,sizeof dist);
dist[1]=0;
for(int i=0;i<n-1;i++)//先找出现在离的最近的且没有放进去的点
{
int t=-1;
for(int j=1;j<=n;j++)//一开始的时候一个点都没有,先确定了1这个点,然后更新1到其他点的距离 ,
if(!st[j]&&(t==-1||dist[t]>dist[j]))
t=j;
for(int j=1;j<=n;j++)//更新距离
dist[j]=min(dist[j],dist[t]+g[t][j]);//第一次循环加入了1这个点,然后开始更新到其他点的距离
st[t]=true;
}
if(dist[n]=0x3f3f3f3f)return -1;
return dist[n];
}
bellman_ford
算法思想遍历所有边,遍历k次找到比较最短路径为k步的最短路径
int n,m;//n表示点数,m表示边数
int dist[N],last[N];//dist[x]存储1到x的最短路径
struct Edge
{
int a,b,w;//a表示入点,b表示出点,w表示权重
}edges[M];
//求1到n的最短路径,如果无法从1走到n,则返回-1;
int bellman_ford()
{
memset(dist,0x3f,sizeof dist);
dist[1]=0;
for(int i=0;i<n;i++)
{
memcpy(last,dist,sizeof dist);//有时候为了避免串联,备份一个上一次的
for(int j=0;j<m;j++)
{
int a=edges[j].a,b=edges[j].b,w=edges[i].w;
if(dist[b]>last[a]+w)
dist[b]=last[a]+w;
}
}
if(dist[n]>0x3f3f3f3f/2)return -1;
return dist[n];
}
spfa
int n;//总点数
int h[N],w[N],e[N],ne[N],idx;//邻接表相关信息
int dist[N],cnt[N];//dist表示最短距离,cnt表示最短路径上经过点数
bool st[N];//表示判断是否在队列
//存在负环返回true,否则返回false;
bool spfa()
{
//不需要初始化dist[]数组
//原理:如果某条最短路径上有n个点,那么加上自己之后一共有n+1个点,那么一定存在负权回路
queue<int> q;
for(int i=1;i<=n;i++)
{
q.push(i);
st[i]=true;
}
while(q.size())
{
auto t=q.front();
q.pop();
st[t]=false;
for(int i=h[t];i!=-1;i=ne[i])
{
int j=e[i];
if(dist[j]>dist[t]+w[i])
{
dist[j]=dist[t]+w[i];
cnt[j]=cnt[t]+1;
if(cnt[j]>=n)return true;
if(!st[j])
{
q.push(j);
st[j]=true;
}
}
}
}
return false;
}
floyd算法
#floyd算法,想象一下以k作为中间节点不断优化
for(int k=1;k<=n;k++)
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
d[i][j]=min(d[i][j],d[i][k]+d[k][j]);
prim算法
int n; // n表示点数
int g[N][N]; // 邻接矩阵,存储所有边
int dist[N]; // 存储其他点到当前最小生成树的距离
bool st[N]; // 存储每个点是否已经在生成树中
// 如果图不连通,则返回INF(值是0x3f3f3f3f), 否则返回最小生成树的树边权重之和
int prim()
{
memset(dist, 0x3f, sizeof dist);
int res = 0;
for (int i = 0; i < n; i ++ )
{
int t = -1;
for (int j = 1; j <= n; j ++ )
if (!st[j] && (t == -1 || dist[t] > dist[j]))
t = j;
if (i && dist[t] == INF) return INF;
if (i) res += dist[t];
st[t] = true;
for (int j = 1; j <= n; j ++ ) dist[j] = min(dist[j], g[t][j]);
}
return res;
}
Kruskal算法
#Kruskal
int n,m;//n为点数,m为边数
int p[N];//并查集的父节点数组
struct Edge//存储边
{
int a,b,w;
}edges[M];
bool cmp(Edge a,Edge b)
{
return a.w<b.w;
}
int find(int x)//并查集查找
{
if(p[x]!=x)p[x]=find(p[x]);
return p[x];
}
int kruskal()
{
sort(edges,edges+m,cmp);
for(int i=1;i<=n;i++);p[i]=i;//并查集初始化
int res=0,cnt=0;//权值和边数
for(int i=0;i<m;i++)//一共m条边
{
int a=edges[i].a,b=edges[i].b,w=edges[i].w;
a=find(a),b=find(b);
if(a!=b)//判断是否在同一个集合//不在则合并
{
p[a]=b;
res+=w;
cnt++;
}
}
if(cnt<n-1)return INF;
return res;
}
染色法判别二分图
int n;//n表示点数
int h[N],e[M],ne[M],idx;//邻接表存储图
int color[N];//表示每个点的颜色,-1表示未染色,0表示白色,1表示黑色
//参数:u表示当前节点,c表示当前颜色
bool dfs(int u,int c)
{
color[u]=c;
for(int i=h[u];i!=-1;i=ne[i])
{
int j=e[i];
if(color[j]==-1)//未染色看以后是否冲突
{
if(!dfs(j,!c))return false;
}
else if(color[j]==c)return false;//已染色判断是否相同,相同则冲突
}
return true;
}
bool check()
{
memset(color,-1,sizeof color);
bool flag=true;
for(int i=1;i<=n;i++)
if(color[i]==-1)
if(!dfs(i,0))
{
flag=false;
break;
}
return flag;
}
匈牙利算法二分图最大匹配
int n1,n2;//n1表示第一个集合中的点数,n2表示第二个集合中的点数
int h[N],e[M],ne[M],idx;
int match[N];//存储第二个集合中每个点当前匹配的第一个集合中是哪个点
bool st[N];//表示第二个集合中的每个点是否被遍历过
int find(int x)
{
for(int i=h[x];i!=-1;i=ne[i])
{
int j=e[i];
if(!st[j])
{
st[j]=true;
if(match[j]==0||find(match[j]))
{
match[j]=x;
return true;
}
}
}
return false;
}
//求最大匹配数,依次枚举第一个集合中的每个点能否匹配第二个集合中的点
int res=0;
for(int i;i<=n1;i++)//也就是最大匹配数
{
memset(st,false,sizeof st);
if(find(i))res++;
} int n1,n2;//n1表示第一个集合中的点数,n2表示第二个集合中的点数
int h[N],e[M],ne[M],idx;
int match[N];//存储第二个集合中每个点当前匹配的第一个集合中是哪个点
bool st[N];//表示第二个集合中的每个点是否被遍历过
int find(int x)
{
for(int i=h[x];i!=-1;i=ne[i])
{
int j=e[i];
if(!st[j])
{
st[j]=true;
if(match[j]==0||find(match[j]))
{
match[j]=x;
return true;
}
}
}
return false;
}
//求最大匹配数,依次枚举第一个集合中的每个点能否匹配第二个集合中的点
int res=0;
for(int i;i<=n1;i++)//也就是最大匹配数
{
memset(st,false,sizeof st);
if(find(i))res++;
}
